다이나믹 프로그래밍은 큰 문제를 작은 문제로 나눠서 생각해야 하는 만큼 각 항목들의 연관성과 규칙을 생각하며 문제를 해결해야 합니다. 다이나믹 프로그래밍 문제를 풀면서 정리해두면 좋을 것 같은 9095, 2156, 1912번 총 3문제의 규칙과 코드를 정리해보겠습니다.
각각의 문제 설명은 연결된 하이퍼링크를 통해 확인하시면 됩니다.
백준 9095번: 1,2,3, 더하기 (다이나믹 프로그래밍)
9095번: 1, 2, 3 더하기
각 테스트 케이스마다, n을 1, 2, 3의 합으로 나타내는 방법의 수를 출력한다.
www.acmicpc.net
다이나믹 프로그래밍은 주어진 숫자 n을 1,2,3으로 표현하는 방법을 찾는 것이 아니라 각 항복들이 어떠한 연결성을 보고 있는지를 찾아야 한다. 따라서 dp[3]까지를 손으로 만들고 규칙성을 찾아보았다.

위의 표에서 볼 수 있듯이 dp[3]은 dp[0], dp[1], dp[2]로 구성할 수 있다. 구성은 다음과 같다.
- dp[0]의 원소에 3을 더한 값
- dp[1]의 원소에 2를 더한 값
- dp[2]의 원소에 1을 더한 값
따라서 dp[3] = dp[2] + dp[1] + dp[0] 으로 표현할 수 있고, 이를 점화식으로 표현하면 아래와 같다.
" dp[i] = dp[i-1] + dp[i-2] + d[i-3] "

dp[4]와 dp[5]의 값을 점화식과 비교해봐도 이상이 없다. 따라서 해당 점화식에 맞게 코드를 작성하면 문제를 해결할 수 있다.
다음은 점화식에 맞게 코드를 작성한 것이다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
# 백준 9095번 1,2,3 더하기(다이나믹 프로그래밍)
t = int(input())
answer = []
for _ in range(t):
answer.append(int(input()))
dp = [1,2,4]
for i in range(3, max(answer)):
dp.append(dp[i-1] + dp[i-2] + dp[i-3])
for i in answer:
print(dp[i-1])
|
이처럼 다이나믹 프로그래밍은 문제의 해결력보다는 관찰력과 논리력을 판단하기 위한 것 같다고 생각된다.
2156번: 포도주 시식
효주는 포도주 시식회에 갔다. 그 곳에 갔더니, 테이블 위에 다양한 포도주가 들어있는 포도주 잔이 일렬로 놓여 있었다. 효주는 포도주 시식을 하려고 하는데, 여기에는 다음과 같은 두 가지 규
www.acmicpc.net
위의 1,2,3 더하기 와는 다르게 포도주 시식은 조건이 있다. 바로 3잔 이상 연속으로 마시면 안 되는 것 다이나믹 프로그래밍에서의 조건은 규칙성을 파악하는데 중요하게 작용한다. 다음은 입력값을 사용한 배열과 함께 정리해놓은 것이다.

"3잔 연속으로 마시지 않는다."라는 조건을 충족하면서 포도주를 마시는 방법은 다음과 같다. 여기서 값은 해당 순서에서 가장 많이 마신 값을 저장하는 dp의 값이다.
- 자신의 포도주를 먹는 방법
- 자신과 자신 전의 포도주를 먹는 방법
- 자신의 포도주를 먹지 않는 방법
다음은 dp[3]까지의 값을 표를 표현한 것이다. 각 dp값은 위의 3가지 방법이 포함되어 있고, 노란색은 그중에서 가장 큰 값을 말한다.
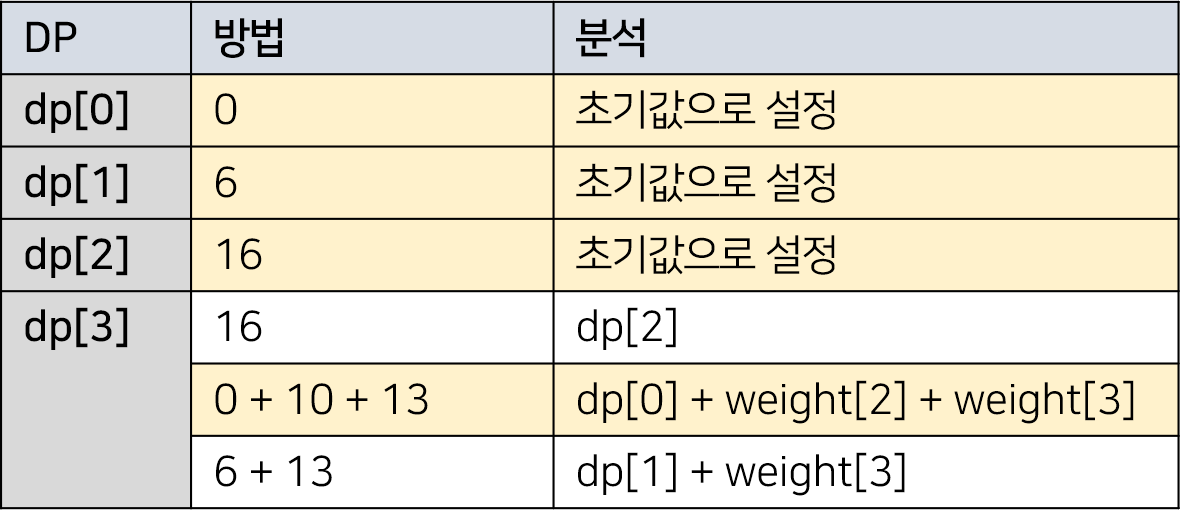
이렇게 수행할 수 있는 방법들 중에 가장 큰 값을 저장하는 방식으로 문제를 해결한다. 여기서 dp[3]을 구하는 공식은 다음과 같다. dp[3] = max(dp[2], dp[0] + weight[2] + weight[3], dp[1] + weight[3]) 해당 식을 점화식으로 만들면 다음과 같다.
" dp[i] = max(dp[i-1], dp[i-3] + weight[i-1] + weight[i], dp[i-2] + weight[i]) "

위의 표는 점화식을 이용하여 최댓값을 구하는 과정이다.
다음은 점화식에 맞게 코드를 작성한 것이다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
# 백준 2156번 포도주 시식(다이나믹 프로그래밍)
n = int(input())
weight = [0]
for _ in range(n):
weight.append(int(input()))
dp = [0]
dp.append(weight[1])
if n > 1:
dp.append(weight[1] + weight[2])
for i in range(3, n+1):
dp.append(max(dp[i-1], dp[i-3] + weight[i-1] + weight[i], dp[i-2] + weight[i]))
print(dp[n])
|
조어진 조건을 활용하여 문제를 해결하는 방식으로 조건에 따른 행동을 생각하면서 문제 해결을 한다면 좋을 것 같다.
2579번: 계단 오르기
계단 오르기 게임은 계단 아래 시작점부터 계단 꼭대기에 위치한 도착점까지 가는 게임이다. <그림 1>과 같이 각각의 계단에는 일정한 점수가 쓰여 있는데 계단을 밟으면 그 계단에 쓰여 있는 점
www.acmicpc.net
포도주 시식과 마찬가지로 해당 문제에도 조건이 3가지 존재한다. 조건은 다음과 같다.
- 계단은 한 번에 한 계단씩 또는 두 계단씩 오를 수 있다. 즉, 한 계단을 밟으면서 이어서 다음 계단이나, 다음다음 계단으로 오를 수 있다.
- 연속된 세 개의 계단을 모두 밟아서는 안 된다. 단, 시작점은 계단에 포함되지 않는다.
- 마지막 도착 계단은 반드시 밟아야 한다.
이 조건 중에서 가장 중요한 조건은 마지막 도착 계단은 반드시 밟아야 한다는 것이다. 마지막 계단을 밟는 방식을 충족하는 점화식을 세워야 한다는 것이다. 이는 다르게 생각해보면 각 항목을 계산할 때 무조건 자신을 밟게 만들면 된다. 자신을 무조건 밟으면서 나머지 조건을 충족하는 방법은 다음과 같다.
- 두 계단을 한 번에 올라 자신을 밟는 방법
- 두 계단을 오른 후 자신과 자신 전의 계단을 밟는 방법
다음은 입력값을 사용한 배열의 이름에 맞게 표시한 것이다.

다음은 answer[3]까지의 값을 표를 표현한 것이다. 각 answer값은 위의 2가지 방법이 포함되어 있고, 노란색은 그중에서 가장 큰 값을 말한다.

여기서 answer[3]의 값을 구하는 방법은 answer[3] = max(answer[1] + data[3], answer[0] + data[2] + data[3])이고, 이 식을 점화식으로 만들면 다음과 같다.
" answer[i] = max(answer[i-2] + data[i], answer[i-3] + data[i-1] + data[i]) "

위의 표는 점화식을 사용하여 최댓값을 구하는 과정이다.
점화식에 맞게 코드를 작성하면 다음과 같다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
# 백준 2579번 계단 오르기 (다이나믹 프로그래밍)
n = int(input())
data = [0] * 301
answer = [0] * 301
for i in range(1,n+1):
data[i] = (int(input()))
answer[0] = 0
answer[1] = data[1]
answer[2] = max(data[0] + data[2], data[1] + data[2])
for i in range(3,n+1):
answer[i] = max(answer[i-2] + data[i], answer[i-3] + data[i-1] + data[i])
print(answer[n])
|
이렇게 총 3가지의 문제에 대한 생각과 풀이를 정리했다. 다이나믹 프로그래밍 문제를 풀어보면서 중요하다고 생각한 부분은 문제를 해결하는 방법보다는 각각의 항목들의 연관성에 대해서 찾는 것을 중점적으로 해결해야 한다는 것이다.
'취업을 준비하며 정리하는 컴퓨터 지식 > Problem Solving' 카테고리의 다른 글
| [Problem Solving] 백준 1916번 최소비용 구하기 문제풀이 (0) | 2021.02.02 |
|---|---|
| [Problem Solving] 백준 1092번 배 문제풀이 (2) | 2021.02.01 |
| [ProblemSolving] 백준 2589번 보물섬 문제풀이 (0) | 2021.01.29 |
| [ProblemSolving] 백준 2667번, 프로그래머스 64061번 문제풀이 (0) | 2021.01.27 |
| [ProblemSolving] 프로그래머스 60057번 문자열 압축 문제풀이 (0) | 2021.01.21 |
